-
Introduction
Understanding how court decisions are made is a major focus of scholarly legal research. The findings of such research can have implications for policy makers wishing to improve legal decisions via guidelines and procedures; practitioners striving to make reliable and justifiable decisions; defendants and victims (or plaintiffs) who directly experience the consequences of court decisions; as well as for those organizations who evaluate and challenge such decisions. Typically, researchers have been critical of both the processes and outcomes of court decisions (e.g., for criticisms of sentencing decisions see Albonetti 1997; Daly & Bordt 1995; Mitchell 2005). However, research on court decisions can itself be criticized, and commentators have pointed to both conceptual and analytic shortcomings of some research (e.g., Britt 2000; Dhami, Belton & Goodman-Delahunty 2015; Dixon 1995).
One major analytic shortcoming is the use of single-level statistical models for court decision data that are actually hierarchically structured (i.e., multilevel; Britt 2000).1x We use the terms hierarchical and multilevel interchangeably. Court decisions are made on individual cases by decision makers sitting in courts located across geographical (or jurisdictional) areas (see Figure 1). This renders a hierarchical data structure where the individual case at the lower level is nested within the higher (contextual) level of the decision makers, who themselves are nested within courts, which are nested within areas. Theoretically, all levels in such a hierarchical structure can have mutual influences upon each other. For example, the effect of offender characteristics (e.g., ethnicity) on sentencing decisions may be influenced by characteristics of the judge (e.g., experience), which in turn may be influenced by characteristics of the court in which the judge sits (e.g., nature of caseload), which in turn may be influenced by the population demographics of the area in which the court is located. Single-level models cannot delineate such effects because they essentially ignore or confound the hierarchical structure of the data.
The hierarchical structure of sentencing data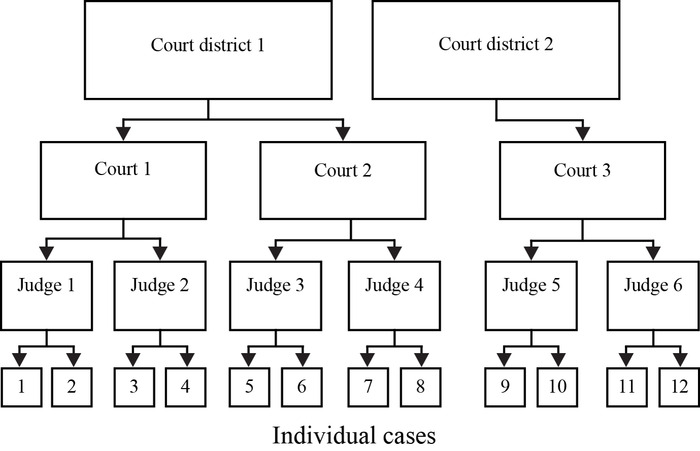
Failing to take the hierarchical structure of the data into account can lead to potentially unreliable and invalid research findings. It can also limit our theoretical and practical understanding of how court decisions are made. For instance, it becomes difficult to measure the extent to which higher-level variables (e.g., judge race) may account for variation in decisions between groups (e.g., White and Black defendants), beyond the influence of lower-level variables (e.g., previous convictions). It also becomes difficult to determine how individual and contextual-level variables may interact to account for variations in decisions. Thus, hierarchically structured court decision data ought to be analyzed using multilevel statistical models (Britt 2000).
The main aim of the present paper is to illustrate when and why multilevel statistical analysis should be used. The remainder of the paper is organized into five sections. We first critically review some examples of past research that has studied sentencing decisions using single-level statistical analyses. We then discuss in detail the problems of conducting single-level analysis on hierarchically structured data. Next, we consider the advantages of conducting multilevel analysis when data are hierarchically structured. Following this, we briefly critically review recent research that has applied multilevel analyses to sentencing data. Finally, we draw some conclusions about the value of conducting statistical analyses appropriately.
-
Statistical Modeling of Court Decisions: The Example of Sentencing
Sentencing decisions can involve choosing among alternative sentence types such as custody, fines, and community penalties, as well as judging the duration or quantity of these sentences (e.g., time in custody or amount of fine; see Dhami & Belton 2015). These decisions may be influenced by a myriad of factors. Grouping these factors into those at the lower (individual) level and higher (contextual) level is pertinent to developing and testing sociolegal theories of sentencing. Lower-level variables include case and defendant characteristics such as offence type, previous convictions, race, and gender. Higher-level variables include judge characteristics such as experience, court variables such as size and caseload, and area-level variables such as crime rate and population demographics.
Sentencing researchers have examined the effect of individual (lower) level variables on sentencing decisions and have also attempted to take account of the influence of many different contextual (higher) level variables. The normal statistical tool used is regression analysis: regression models allow researchers to estimate the linear relationship between a predictor variable (e.g., previous convictions) and an outcome variable (e.g., custodial sentence length), when all other potential predictor variables are held constant. However, until relatively recently, researchers typically confounded the influence of higher- and lower-level variables by using single-level statistical models such as ordinary least squares (OLS) regression and logistic regression.
For example, Steffensmeier, Kramer and Streifel (1993) studied the effect of offender gender on sentence type (i.e., probation, jail, or prison) and sentence length in Pennsylvania. Their data were clearly hierarchical: they included offender characteristics such as race, age, and criminal history, as well as six contextual variables (i.e., judges’ workload, type of disposition (trials vs. guilty pleas), and percentage of urban dwellers, Black population, Republican supporters, and population aged 15–19 years). However, the authors used logistic regression and OLS regression to analyze their data. They found that the decision to imprison/jail versus give probation was predominantly influenced by offence seriousness and the offender’s criminal history. The offender’s gender and other characteristics also influenced the decision but to a much smaller extent, as did all contextual variables except judges’ workload. Sentence length was also predicted most strongly by offence seriousness and criminal history. The effect of gender and other offender characteristics was negligible. Of the contextual factors, only disposition type and percentage of Republican supporters significantly predicted a longer sentence, and their effect was small. The regression models showed that offender gender also interacted with other variables, in particular, sentence severity, with females receiving slightly shorter sentences for serious offences but slightly longer sentences for more minor offences.
In another example, Williams (2003) studied decisions to incarcerate adult felony cases in Florida where the offender had pled guilty. He used logistic regression and OLS regression to measure the predictive value of pretrial detention as well as other variables (i.e., bail status, offence type, number of felony charges, number of prior felony convictions, attorney type, length of disposition, race/gender of defendant, age of defendant) on incarceration and custodial sentence length, respectively. Here, despite attorney type (i.e., private versus appointed attorney) being a higher-level variable, Williams used single-level analysis. Logistic regression analysis revealed that pretrial detention, offence type, number of prior felony convictions, and race/gender of defendant were significant predictors of incarceration, whereas the other variables (including attorney type) were not. Similarly, results from the OLS regression indicated that whereas pretrial detention, offence type, number of felony charges, length of disposition, and race/gender of defendant were significant predictors of sentence length, attorney type was not.
More recently, Schanzenbach (2015) studied the extent to which racial disparities in US federal sentencing are due to judge-related factors (i.e., race and political affiliation) and two structural factors relating to the sentencing system (i.e., a stricter standard of review for departures from sentencing guidelines and rulings declaring the guidelines are advisory only). Using OLS regression, Schanzenbach found that a judge’s political affiliation was associated with offence-level calculations, custodial sentence length, and departures from the guidelines. A judge’s race was not associated with custodial sentence length or downward departures, but was with offence-level calculations. Finally, these effects were not related to changes in the structural factors studied. However, the reliability and validity of these findings are threatened by the fact that Schanzenbach used single-level analysis of data that is clearly hierarchically structured.
-
Problems with Applying Single-Level Statistical Models to Hierarchical Data
Performing single-level statistical analysis on hierarchically structured data is inappropriate because some essential statistical assumptions of single-level statistical models such as OLS regression are violated (for more details see e.g., Bryk & Raudenbush 2002; Goldstein 2011; Hox 2010; Rasbash et al. 2005; Tabachnick & Fidell 2014). OLS regression uses residual errors—the distance of individual data points from the line predicted by a regression model—to evaluate how well the model fits the data overall. An OLS model assumes that all data at one level (e.g., about offenders) are independent of each other and their residual errors are uncorrelated. However, when data are hierarchical (e.g., offenders grouped within courts), residual errors are likely to be correlated within groups. For example, sentencing practice within one court is likely to be similar because of comparable training and experiences of judges in that court, but may differ from the sentencing practice of judges in another court. Treating residual errors as independent when they are not artificially inflates the likelihood of obtaining statistically significant results.
OLS regression assumes that there are low levels of collinearity (intercorrelation) between predictors. However, hierarchical data mean that predictor variables across levels are likely to be correlated. For example, workload and stress level are likely to be correlated when measuring the number of cases sentenced by judges (where court workload is a higher-level variable and judges’ stress level is a lower-level variable). In single-level models, highly correlated predictors do not contribute uniquely to the variable being predicted, and so the effect of one variable cannot be separated from the effect of the other. In addition, high collinearity means that regression coefficients (the statistics that indicate the extent to which a variable predicts a given outcome) are more likely to be statistically nonsignificant.
OLS regression also assumes homoscedasticity of the data (i.e., the variance of residual errors is spread equally around all the predictors). However, hierarchical data involve different groups, often of different sizes, and so the spread of variance around each group is different. For example, if court size is a predictor and we know that urban courts are larger than rural courts, then the variance spread around court size will be different for urban and rural courts. When homoscedasticity is violated, heteroscedasticity is present, and in single-level models this threatens the validity of the results by reducing the strength of the findings and invalidating tests of statistical significance and related confidence intervals.
Beyond violating statistical assumptions, there are other problems with applying single-level statistical models to hierarchically structured data. In hierarchical data, variance can occur at lower levels (or within groups) and at higher levels (or between groups). For example, the total variability in national sentence lengths can be split into variability of sentencing within each court and variability of sentences between courts. OLS regression cannot partition the variance across those two levels, and this inability to partition the variance typically causes effects at all levels to appear more statistically significant than they truly are.
The importance of each individual predictor variable within a regression model is represented by its regression coefficient, which describes how much the outcome variable changes as a function of changes in that predictor variable. OLS cannot establish heterogeneous regression coefficients; in other words, it cannot allow for the fact that the relationship between a lower-level predictor variable and an outcome variable may differ across higher-level groups. For example, race or gender may relate differently to incarceration rates depending on the court in which a case is sentenced.
As a way of incorporating naturally hierarchical data into a single-level structure, single-level models often use the procedures of aggregation or disaggregation. Aggregation is the process of creating higher-level variables from lower-level ones by summarizing the latter. For example, aggregation may be done by computing the court mean of judges’ experience, so that this variable, originally a judge-level variable, becomes a higher, court-level variable. In contrast, disaggregation involves deconstructing higher-level variables into lower-level ones. For example, this may be done by assigning all judges in a court the mean caseload from their court, so this higher-level variable becomes a lower-level variable. Aggregation and disaggregation mean that variables are not analyzed at their original level of measurement, and this can create several problems.
Aggregation leads to many data units at the lower level being replaced by fewer data units at the higher level, resulting in a loss of information and reduction of statistical power. It also leads to the ‘atomistic fallacy,’ which is drawing conclusions about the relations between higher-level variables when they are actually created from lower-level variables. Imagine, for example, that one calculated mean custodial sentence length and judges’ mean experience for several court districts. Both of these variables are higher-level variables created by aggregating lower-level data (i.e., individual sentence lengths and individual judges’ experience). This is different from a true higher-level variable such as court size or caseload. One cannot infer the relationship between mean sentence length and mean judges’ experience in that district based on the relationship between the length of sentences meted out by individual judges and their experience.
Conversely, disaggregation leads to few higher-level data units being magnified into a much larger number of lower-level data units, which in turn inflates the chances of obtaining statistically significant results. Disaggregation also leads to the ‘ecological fallacy,’ which is drawing conclusions about relations between lower-level variables created from higher-level variables. For example, one cannot infer the relationship between an individual defendant’s length of trial and his/her sentence length based on the relationship between mean length of trial in a court and mean length of sentence given in that court. Courts that, on average, hold longer trials may mete out longer sentences, but it could be that within any given court, a shorter trial is associated with a longer sentence.
Finally, single-level regression analysis can be used to establish the extent of differences between groups in hierarchical data by using a fixed effects model. Regression coefficients are fixed and not allowed to vary randomly. To fit higher-level data, the fixed effects model uses dummy variables for each higher-level variable. The regression coefficients of the dummy variables provide estimates of higher-level effects. The shortcoming of the fixed effects model is that it does not allow generalization to the population since the groups are not treated as random samples of the population and group effects are fixed (rather than random).2x For more information on fixed and random effects models in applied research see Clarke et al. 2010. Also, this model is not designed for a large number of groups or for small numbers of lower-level variables in each higher-level group. Furthermore, the fixed effects model does not allow higher-level predictors to be introduced into the equation because the degrees of freedom in the model are fully used.
Based on the above, we can identity several threats to the reliability and validity of the findings of the three examples of sentencing research described earlier that applied single-level statistical analyses to multilevel data. For instance, Steffensmeier et al. (1993) found that all the case-level variables tested influenced the decision to imprison, including criminal history, offence type, and gender. However, nonindependence of residual errors and/or the inability to partition variance could both have artificially increased the likelihood of the predictors being found to have a significant effect. In addition, the findings for individual-level variables may have been inaccurate for several reasons, including that each variable may have needed a different regression coefficient for each higher-level group (e.g., the effect of an offender’s gender on whether they received a prison sentence may have differed across courts or court districts). Conversely, high collinearity among contextual-level variables such as judges’ workload and disposition type could have produced falsely nonsignificant results for those variables. Heteroscedasticity could also have reduced the likelihood of finding a significant result for contextual variables. Williams (2003) found that attorney type was not a significant predictor of sentence length among guilty plea felony cases in Florida. However, attorney type could have been strongly correlated with relevant characteristics of the offender and the resulting collinearity may have rendered the result nonsignificant. The findings could also have been weakened by heteroscedasticity produced by a difference in the numbers of private and appointed attorneys. Finally, similar criticisms can be leveled at Schanzenbach’s finding that changes in wider structural factors did not alter the effects of the judge-level factors studied (for a further critique, see Dhami 2015).
-
The Value of Multilevel Statistical Models
The solution to the problem of analyzing hierarchically structured data is to perform multilevel analysis such as multilevel logit and multilevel regression analyses (see Bryk & Raudenbush 2002; Goldstein 2011; Hox 2010; Rasbash et al. 2005; Tabachnick & Fidell 2014). To overcome the problem of correlated residual errors, multilevel analysis introduces a unique random effect for each higher-level group. The random effect accounts for the lack of independence of observations and the grouped nature of hierarchical data. A model that includes unique random effects allows for more accurate measurement of standard errors and parameter estimates and thus more precise statistical significance testing.
To overcome the problem of collinearity, multilevel analysis centers individual scores of lower-level variables around the grand mean. Centering scores around the grand mean is a variable transformation technique that leads to standardized scores. It involves subtracting a single grand mean score from each score recorded for each level 1 variable regardless of groups (e.g., if the grand mean for previous convictions was 2, then an offender with 3 previous convictions would have his score adjusted to 1; 3 minus 2). Thus, the raw scores of the parameters change to the grand mean centered scores. Measures of model fit, outcome scores, and residual errors remain the same for grand mean centered scores and raw scores. Grand mean centering also stabilizes the analysis.
The problem of heteroscedasticity is dealt with by introducing random error into the model. The random error term for a group is assigned to every individual-level data unit in that group. Thus, random errors are different for lower-level predictors belonging to different groups. The random errors are able to account for different variances occurring as a result of group differences in hierarchical data.
Multilevel analysis can partition the total variance of the outcome variable(s) into between- and within-groups variances. This makes it possible to account for the amount of variance occurring as a result of between-group differences and within-group differences. Also, the partitioning of variance enables calculation of the intraclass correlation, which is the degree of similarity between values of the outcome variable for lower-level predictors belonging to the same higher-level group. In addition, the intraclass correlation measures the proportion of variance that can be accounted for by higher-level predictors.
Regression coefficients in multilevel analysis are heterogeneous since they are designed to account for different groups forming a hierarchical structure. Separate regression coefficients for each group allow modeling of variation in the effects of lower-level predictors across groups.
Multilevel analysis does not require aggregation and disaggregation since it can deal with data at its original level without the need to move data from one level to another. Lower-level data remain at the lower-level and higher-level data remain at the higher level in multilevel analysis.
Finally, multilevel analysis involves random effects models. Unlike fixed effects models, random effects models allow for generalization because groups in multilevel analysis are treated as random groups taken from a population of groups, and so the group effects are random. Multilevel analysis can also take into account a large number of groups. Furthermore, higher-level predictors can be introduced into the model directly, which means that the model can account for the grouping nature of the data and no additional degrees of freedom are required.
In sum, multilevel analysis overcomes the limitations of single-level analysis, and contextual influences on court decisions can be properly ascertained (Britt 2000). Indeed, multilevel (as opposed to single-level) theories of sentencing decisions can highlight both the effect of lower-level variables such as case and defendant characteristics, as well as the direct and moderating effect of higher-level variables such as judge, court, and area on sentencing decisions. Prominent examples of multilevel theories include racial threat (Blalock 1967), court community (Eisenstein, Flemming & Nardulli 1988), uncertainty avoidance (Albonetti 1991), and focal concerns (Steffensmeier, Ulmer & Kramer 1998). Multilevel theories can, therefore, offer more comprehensive accounts of sentencing.
-
How to Apply Multilevel Models
Several bespoke statistical software packages have been developed to compute multilevel models (see Bryk & Raudenbush 2002; Goldstein 2011; Rasbash et al. 2005). In addition, most major statistical packages such as SPSS, STATA, and SAS also contain modules for analyzing multilevel data.
Multilevel analysis can be applied to various different predictor variables at different levels. For example, using the levels in Figure 1, individual case-level variables could include offender characteristics such as race, gender, age, and previous convictions. Judge-level variables could include race, gender, experience, and political affiliation. Court-level variables could include court size and workload. Finally, district-level variables could include crime rate, incarceration rate, and the percentage of ethnic minorities in the district.
Multilevel analysis can also be applied to a range of different outcome variables that are observed in the criminal justice system (with different types of multilevel models being applied to different types of outcome variables). These can include continuous outcomes such as length of custody or amount of fine; binary and proportion outcomes such as decisions to parole or not; nominal outcomes such as different types of community sentences; and ordinal outcomes such as punitiveness of remand decision.
Briefly, to carry out multilevel analysis, the first step is to build an unconditional model, which estimates the amount of variation in the outcome variable that is occurring at each level of analysis (for more details see Bryk & Raudenbush 2002; Goldstein 2011; Hox 2010; Rasbash et al. 2005; Tabachnick & Fidell 2014). This highlights the relative importance of lower- and higher-level variables, and provides a baseline against which models containing lower- and higher-level predictors can be assessed. Next, level 1 predictors are introduced into the model to estimate their direct effects on the outcome variable. This also shows the degree to which effects of level 1 predictors vary across groups and also the degree to which the outcome varies across groups when level 1 predictors are included. Then, level 2 predictors (e.g., judge race and experience) are introduced into the model to assess the direct effects of higher-level predictors on the outcome variable and to measure the degree to which higher-level predictors influence variations at the lower level. Also, the full model containing both level 1 and 2 predictors includes the cross-level interactions that specify how the effects of lower-level predictors may be moderated or conditioned by higher-level predictors. For data that have more than two levels, additional levels of predictors are simply added one-by-one until all the data are included in the model.
-
Observations on Sentencing Research Using Multilevel Models
Earlier, we provided examples of sentencing studies that have misapplied single-level models to hierarchically structured data (Schanzenbach 2015; Steffensmeier et al. 1993; Williams 2003). Fortunately, an increasing number of sentencing researchers are now using multilevel models (e.g., Anderson & Spohn 2010; Farrell, Ward & Rousseau 2009; Feldmeyer & Ulmer 2011; Haynes, Ruback & Cusick 2010; Johnson, Ulmer & Kramer 2008; King, Johnson & McGeever 2010; Pina-Sánchez & Linacre 2013; Ulmer & Johnson 2004; Ulmer, Light & Kramer 2011; Wooldredge, Griffin & Thistlethwaite 2013). They recognize the necessity of analyzing sentencing data using multilevel models to explore the effects of both higher- and lower-level variables and the relationships between them. In fact, multilevel analysis can now reasonably be described as a ‘mainstream tool’ within the field of sentencing research (Pina-Sánchez & Linacre 2013, p. 1122).
To illustrate the benefits of using multilevel analysis, we describe the study conducted by Feldmeyer and Ulmer (2011) that tested the ‘racial threat’ hypothesis. This predicts a curvilinear relationship between the size of racial or ethnic minority populations in a community and sentencing disparities between racial/ethnic minority offenders and majority White offenders. In other words, it is predicted that as the relative size of the ethnic population to Whites increases, so will the disparity in sentencing for ethnic and White offenders (i.e., harsher sentences for ethnic minorities in an effort to control them), until the ethnic population reaches a sufficient size enabling them to contest such social control, and so sentencing disparities between ethic and White offenders decrease. Testing the racial threat hypothesis requires examining the interaction between individual- and contextual-level variables (i.e., offender race/ethnicity and racial/ethnic minority population percentage), while taking into account the effects of other individual- and contextual-level variables.
Feldmeyer and Ulmer used a two-level hierarchical linear regression model to examine 131,672 cases across US 89 federal districts. The model incorporated 23 individual-level predictors including offender race/ethnicity. The effects of offender race/ethnicity were allowed to vary between districts, whereas the effects of other individual-level predictors were fixed. Sixteen district-level predictors were also studied. These included percentage of Black or Hispanic population and minority population quartiles. Ten cross-level interaction effects between offender race/ethnicity and district race/ethnicity were also examined: Black offender by Black population proportions (overall percentage, percentage squared, and first, second, and third quartiles), and the same for Hispanic offenders. The outcome variable was custodial sentence length in months, centered around district-level group means.
Feldmeyer and Ulmer found that 93% of the variation in sentence length occurred across individuals, and 21 of the 23 individual-level variables—including the offender being Black (but not Hispanic)— were significant predictors of sentence length. In addition, racial and ethnic sentencing disparities were found to vary significantly across districts. Six of the 16 district-level variables were significant predictors of custodial sentence length but this did not include any of the minority population measures. In addition, the interactions between Black offender and Black population percentages were nonsignificant, whereas Hispanic offenders were found to be sentenced more harshly in districts with Hispanic populations of 1% to 3% or 9% to 27% than in those districts with a Hispanic population of 4% to 8% or 28+%. Thus, Feldmeyer and Ulmer were able to conclude that there was no evidence from the federal courts to confirm the racial threat hypothesis for Black offenders, and for Hispanic offenders the evidence suggested that although there is a relationship between minority percentage quartile and sentencing severity, it is not curvilinear as postulated.
-
Room for Improvement in Multilevel Studies of Sentencing
Although there is a growing body of research applying multilevel models to the study of sentencing decisions, this research also has some limitations that ought to be addressed if future research is to benefit from the full potential of multilevel analysis. First, very few studies (e.g., Ulmer & Johnson 2004) have used the deviance statistic to measure the fit of their models (models with lower deviances fit the data better than those with higher deviance). Often, several models are tested in a study, for example, a model that only includes individual-level variables, then a model that includes both individual and court-level variables, and finally a model that includes both levels of variables as well as selected cross-level interaction effects. However, authors may only report the deviance statistic for one stage of model development. Thus, most published studies do not clearly specify which of the models best fits their data.
Second, researchers have typically not explored all possible cross-level interaction effects (e.g., Feldmeyer & Ulmer 2011), and many recent multilevel studies have not explored any (e.g., Ulmer et al. 2011). Although this is defensible on grounds of parsimony and in terms of studying only theoretically relevant interactions, this practice may nevertheless limit our understanding of sentencing, especially to the extent that macrolevel theories are restricted to specific sets of variables.
Third, multilevel analyses are not immune from aggregation. For instance, Johnson et al. (2008) aggregated crime rate data from county to district level for comparison with other district-level variables. Feldmeyer and Ulmer (2011) aggregated some case and county-level data to the district level. Although there may be practical reasons for aggregating higher levels, it conflicts with the rationale for conducting multilevel analysis. One way of reducing the number of levels in a model may be to develop theories that clearly specify the level at which particular variables should be analyzed.
Finally, although multilevel research has revealed that there is a sociocultural dimension to sentencing decisions, involving contextual variables such as the race, gender, and experience of judges and other court workers, court caseloads, and neighborhood deprivation (e.g., King et al. 2010; Farrell et al. 2009; Haynes et al. 2010; Wooldredge et al. 2013; Wooldredge & Thistlethwaite 2004), it also suggests that the influence of higher-level variables should not be overstated. A recent review of 28 multilevel studies of sentencing (Dhami & Belton 2016) found that although many higher-level variables were statistically significant predictors of sentencing, they typically accounted for less than 10% of the variance in sentencing outcomes, and sometimes substantially less. For instance, Pina-Sánchez and Linacre (2013) reported that only 1.8% of the variance in sentencing decisions across Crown Courts in England and Wales could be accounted for by differences between courts.
This body of research, therefore, strongly suggests that individual (case) level variables are by far the dominant predictors of sentencing decisions. On the other hand, the relative lack of predictive power found for the higher-level variables tested to-date may also indicate that the most informative variables have not yet been identified, perhaps because macrolevel or multilevel theories of sentencing are still incomplete. Several sociolegal theories have been tested that postulate the importance of contextual variables, including racial threat (Blalock 1967), court community (Eisenstein et al. 1988), uncertainty avoidance (Albonetti 1991), and focal concerns (Steffensmeier et al. 1998); however, the development of a more comprehensive and precise theory of how higher-level variables may affect sentencing decisions is warranted.
-
Concluding Remarks
Understanding how courts make decisions such as how they sentence offenders can prove very useful for policy and practice. The fact that court decision-making data is intrinsically structured in a hierarchical way, however, has proved challenging for some researchers. Some studies of sentencing, for example, have incorrectly applied single-level statistical models to such data. This approach either ignores or confounds the influence of higher-level (contextual) variables and can potentially lead to unreliable and invalid findings, as well as to a limited theoretical and practical understanding of how court decisions are made. Multilevel statistical models are designed to examine hierarchal data. In the present paper, we have attempted to describe when and why such analysis is necessary. Analyzing data using the appropriate tools is one step toward expanding our knowledge of behavior in legal domains where the data are hierarchically structured and where contextual variables may influence case-level outcomes.
References Albonetti 1991
C.A. Albonetti, ‘An Integration of Theories to Explain Judicial Discretion’, Social Problems (38) 1991, p. 247-266.Albonetti 1997
C.A. Albonetti, ‘Sentencing under the federal sentencing guidelines: Effects of defendant characteristics, guilty pleas, and departures on sentence outcomes for drug offenses’, Law and Society Review (31) 1997, p. 789-822.Anderson & Spohn 2010
A.L. Anderson & C. Spohn, ‘Lawlessness in the federal sentencing process: A test for uniformity and consistency in sentence outcomes’, Justice Quarterly (27) 2010, p. 362-393.Blalock 1967
H.M. Blalock, Toward a theory of minority group relations, New York: Wiley 1967.Britt 2000
C.L. Britt, ‘Social context and racial disparities in punishment decisions’, Justice Quarterly, (17) 2000, p. 707-732.Bryk & Raudenbush 2002
A.S. Bryk & S.W. Raudenbush, Hierarchical linear models: Applications and data analysis methods (2nd ed.), London: Sage 2002.Clarke et al. 2010
P. Clarke, C. Crawford, F. Steele, & A. Vignoles, The choice between fixed and random effects models: Some considerations for educational research, IZA Discussion Paper No. 5287, Bonn, IZA 2010.Daly & Bordt 1995
K. Daly & R.L. Bordt, ‘Sex effects and sentencing: An analysis of the statistical literature’, Justice Quarterly (12) 1995, p. 141-175.Dhami 2015
M.K. Dhami, ‘Racial disparities, judge characteristics, and standards of review in sentencing: comment’, Journal of Institutional and Theoretical Economics (171) 2015, p. 48-52.Dhami & Belton 2015
M.K. Dhami, & I. Belton, I.’ Using court records for sentencing research: Pitfalls and possibilities.’ In J. Roberts (Ed.), Exploring sentencing in England and Wales (pp. 18-34). Palgrave Macmillan 2015.Dhami & Belton 2016
M.K. Dhami & I. Belton, A review of multilevel studies of sentencing, unpublished manuscript 2016.Dhami, Belton & Goodman-Delahunty 2015
M.K. Dhami, I. Belton & J. Goodman-Delahunty, ‘Quasirational models of sentencing’, Journal of Applied Research in Memory and Cognition (4) 2015, p. 239-247.Dixon 1995
J. Dixon, ‘The organizational context of criminal sentencing’, American Journal of Sociology (100) 1995, p. 1157-1198.Eisenstein, Flemming & Nardulli 1988
J. Eisenstein, R. Flemming & P. Nardulli, The contours of justice: Communities and their courts, Boston: Little, Brown 1988.Farrell, Ward & Rousseau 2009
A. Farrell, G. Ward & D. Rousseau, ‘Race effects of representation among federal court workers: Does black workforce representation reduce sentencing disparities?, The Annals of the American Academy of Political and Social Science (623) 2009, p. 121-133.Feldmeyer & Ulmer 2011
B. Feldmeyer & J.T. Ulmer, ‘Racial/ethnic threat and federal sentencing’, Journal of Research in Crime and Delinquency (48) 2011, p. 238-270.Goldstein 2011
H. Goldstein, Multilevel statistical models (4th ed.), Chichester: John Wiley and Sons 2011.Haynes, Ruback & Cusick 2010
S.H. Haynes, B. Ruback & G.R. Cusick, ‘Courtroom workgroups and sentencing’, Crime & Delinquency (56) 2010, p. 126-161.Hox 2010
J. Hox, Multilevel analysis: Techniques and applications (2nd ed.), Hove: Routledge 2010.Johnson, Ulmer & Kramer 2008
B.D. Johnson, J.T. Ulmer & J.H. Kramer, ‘The social context of guidelines circumvention: The case of federal district courts’, Criminology (46) 2008, p. 737-783.King, Johnson & McGeever 2010
R.D. King, K.R. Johnson & K. McGeever, ‘Demography of the legal profession and racial disparities in sentencing’, Law & Society Review (44) 2010, p. 1-32.Mitchell 2005
O. Mitchell, ‘A meta-analysis of race and sentencing research: Explaining the inconsistencies’, Journal of Quantitative Criminology (21) 2005, p. 439-466.Pina-Sánchez & Linacre 2013
J. Pina-Sánchez & R. Linacre, ‘Sentence consistency in England and Wales: Evidence from the Crown Court sentencing survey’, British Journal of Criminology (53) 2013, p. 1118-1138.Rasbash et al. 2005
J. Rasbash et al., A user’s guide to MLwiN, version 2.0., University of Bristol: Centre for Multilevel Modelling 2005.Schanzenbach 2015
M.M. Schanzenbach, ‘Racial disparities, judge characteristics, and standards of review in sentencing’, Journal of Institutional and Theoretical Economics (171) 2015, p. 27-47.Steffensmeier, Kramer & Streifel 1993
D. Steffensmeier, J. Kramer & C. Streifel, ‘Gender and imprisonment decisions’, Criminology (31) 1993, p. 411-446.Steffensmeier, Ulmer & Kramer 1998
D. Steffensmeier, J. Ulmer, & J. Kramer, ‘The interaction of race, gender, and age in criminal sentencing: The punishment cost of being young, black, and male’, Criminology (36) 1998, p. 763-797.Tabachnick & Fidell 2014
B.G. Tabachnick & L.S. Fidell, Using multivariate statistics (6th ed.), Harlow, Essex: Pearson Education 2014.Ulmer & Johnson 2004
J.T. Ulmer & B. Johnson, ‘Sentencing in context: A multilevel analysis’, Criminology (42) 2004, p. 137-177.Ulmer, Light & Kramer 2011
J.H. Ulmer, M.T. Light & J. Kramer, ‘The ‘liberation’ of federal judges’ discretion in the wake of the Booker/Fanfan decision: Is there increased disparity and divergence between courts?’, Justice Quarterly (28) 2011, p. 799-837.Williams 2003
M.R. Williams, ‘The effect of pretrial detention on imprisonment decisions’, Criminal Justice Review (28) 2003, p. 299-316.Wooldredge, Griffin & Thistlethwaite 2013
J. Wooldredge, T. Griffin & A. Thistlethwaite, ‘Comparing between-judge disparities in imprisonment decisions across sentencing regimes in Ohio’, The Justice System Journal (34) 2013, p. 345-368.Wooldredge & Thistlethwaite 2004
J. Wooldredge & A. Thistlethwaite, ‘Bilevel disparities in court dispositions for intimate assault’, Criminology (42) 2004, p. 417-456.-
1 We use the terms hierarchical and multilevel interchangeably.
-
2 For more information on fixed and random effects models in applied research see Clarke et al. 2010.
Citeerwijze van dit artikel:
Mandeep Dhami and Ian Keith Belton, ‘Statistical Analyses of Court Decisions: An Example of Multilevel Models of Sentencing’, 2016, oktober-december, DOI: 10.5553/REM/.000019
Law and Method |
|
| Artikel | Statistical Analyses of Court Decisions: An Example of Multilevel Models of Sentencing |
| Authors | Mandeep Dhami en Ian Keith Belton |
| DOI | 10.5553/REM/.000019 |
|
Show PDF Show fullscreen Abstract Statistics Citation |
| This article has been viewed times. |
| This article been downloaded 0 times. |
Mandeep Dhami and Ian Keith Belton, 'Statistical Analyses of Court Decisions: An Example of Multilevel Models of Sentencing', LaM October 2016, DOI: 10.5553/REM/.000019
|
Quantitative empirical research into legal decisions must be conducted using statistical tools that are appropriate for the data involved. Court decisions are one example of a domain where the data is intrinsically hierarchical (i.e., multilevel), since decisions are made on individual cases by decision-makers in courts located across geographical (or jurisdictional) areas. Past research into court decisions has often either neglected higher level variables or incorrectly used single-level statistical models to analyze multilevel data. The lack of a clear understanding about when and why multilevel statistical models are required may have contributed to this situation. In this paper, we identify the problems of estimating single-level models on hierarchically structured data, and consider the advantages of conducting multilevel analyses under these circumstances. We use the example of criminal sentencing research to illustrate the arguments for the use of multilevel models and against a single-level approach. We also highlight some issues to be addressed in future sentencing studies. |
Dit artikel wordt geciteerd in
- Introduction
- Statistical Modeling of Court Decisions: The Example of Sentencing
- Problems with Applying Single-Level Statistical Models to Hierarchical Data
- The Value of Multilevel Statistical Models
- How to Apply Multilevel Models
- Observations on Sentencing Research Using Multilevel Models
- Room for Improvement in Multilevel Studies of Sentencing
- Concluding Remarks
- References
- ↑ Back to top

